2019-01-05

強化学習（TD3）を試したら環境依存性が強くてビックリしたという話

今回のポストは、TD3 という手法を試してみたら論文通りの性能が出ずに悩んでいたんですが、その原因が環境差にあったという笑えない話です。

経緯

ロボット動作などの、連続行動空間での強化学習にはPPOが今のところ最強なのではないかと思っていたのだけど、TD3の論文 (Addressing Function Approximation Error in Actor-Critic Methods: https://arxiv.org/pdf/1802.09477.pdf)を見ると、様々なタスクでTD3がPPOを大きく上回っているではありませんか。これは試す価値があるなと思って、TD3をchainer で自作して Walker2d で試してみました。

ところが、論文のような学習効果が全くでないんです。

Pendulum などの小さな問題ではきちんと学習できていますし、一通りのバグチェックもしましたが、どうしても誤りを見つけることができませんでした。

最後に残った可能性は次の二つでした。

論文著者はpytorchを使用している（
GitHub - sfujim/TD3: PyTorch implementation of TD3 and DDPG for OpenAI gym tasks
）が、私はchainer を使った。
OpenAI gym の mujoco Walker2d-v1 でなく、DartWalker2d-v1 を使っている。

Pytorch でなく chainer を使っている

Pytorch と Chainer の違いを調べたのですが、私が使った機能の範囲では、全結合層の重みの初期化方法が異なることだけしか違いがるようには見えませんでした。

重みの初期化については、pytorch 方式に合わせて、私のプログラムを修正しましたが、結果は変わりませんでした。

OpenAI gym の mujoco Walker2d-v1 でなく DartWalker2d-v1 を使っている

OpenAI gym の Walker2d-v1 を動かすには mujoco という物理エンジンが必要ですが、mujoco はフリーソフトではありません。私はサラリーマンのオジサンですから無料の Student Licenceは使えません。$500/year とはいえライセンス費用を支払うのもキツイですし、mujoco の無償お試しを使うのも面倒なので、mujoco とほぼ同じ結果になるとされている DartEnv を使っていました。

github.com

Walker などの接触拘束が多い場面では mujoco と Dart に完全互換はあり得ませんが、制御レベルからみれば同じとみなせる仮想環境であろうと考えていました。

ところが、です。

TD3の作者が公開している pytorch 実装で、mujoco Walker2d-v1 でなく、DartWalker2d-v1 の学習を実行させてみたら、学習は論文通りには進まなかったのです・・・。（Fig. 1）

学習曲線も私の実装したプログラムの結果と瓜二つ。論文著者のプログラムであっても、DartWalker2d はうまく学習できなかったということです。

f:id:FakeOwl:20190104234820p:plain — Fig.1 学習曲線

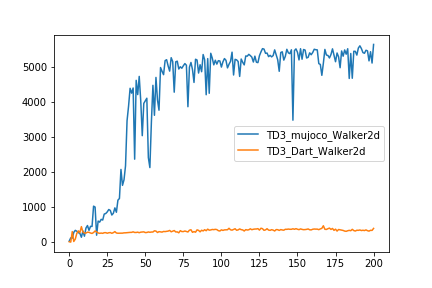
ええ！？って感じですよね。

環境依存性がこんなに大きくていいのかよ！？って思いました。

利用者としての意見

強化学習はパラメータに敏感で怖いなって思いますけど、今回はまた別の意味での脆弱さを感じました。

私が今回感じた課題は２つです。

シミュレーション環境の差で、学習性能がこれほど変わるようなアルゴリズムでは使いにくい。
強化学習の性能評価に用いる仮想環境は、もっと詳細な議論や調査が必要。

１.に関しては、PPOなどの他のアルゴリズムでは環境依存性がどの程度あるのか試していませんが、環境が少し変わっただけで学習が進まなくなるようなアルゴリズムは使い勝手が悪すぎるなという印象です。

連続行動空間での強化学習の論文では、今のところ、mujoco の hopper や walker などがデファクトの例題となっていますが、実世界応用を考えたときに、mujocoの例題だけではアルゴリズムの評価はできてないんじゃないの？と疑問を持たざるを得ません。

２．については、強化学習の利用者からすると、是非クリアになっていってほしい課題です。

mujoco と Dart との、何の差がこれほどまでの学習進捗の差を生み出したのかを把握したいです。これをクリアにしておかないと、どのような基準を満たすシミュレーションで事前検討を進めればよいのか分かりません。

強化学習を現実世界に適用（例えば２足歩行ロボット）することを想定した場合、プロトタイプ作成前に、シミュレーション環境で学習効率や制御性能を検討しようと考えるのはよくあることだと思いますが、その際にシミュレータが満たすべき性能／信頼性のポイントが不明なままでは、シミュレータでの学習検討の意味はあまりないように思います。

2018-11-26

Exploration by Random Network Distillation の効果を MountainCar で試した。

Reinforcement Learning

強化学習を実際にやってみようと思った人なら、誰でも（？）知っている Atari の Motezuma's Revenge 。

ランダムプレイでは攻略のヒントがつかめないので、強化学習で攻略するには難しいタイプの問題として有名なゲームですね。

この Montezuma's Revenge が、かなり簡単な工夫で攻略されているという記事が興味を引いたので、実際に自分でも試してみました。

gigazine.net blog.openai.com

テスト問題

テスト問題には、OpanAI gym の MountainCar-v0 を選びました。

強化学習をやろうとしている人なら MountainCar は知っていると思うので説明はいらないと思うけど、この問題は、非力な車を前後に加速して山を登り切ったら完了、というものです。

この車には停止状態から坂を上りきるだけの推力がないので、前後に動きながら勢いを増していかないと坂を上りきることができません。
複雑な問題ではけれど、ゴールにたどり着くまでは意味のある報酬が得られない疎な報酬設定の問題で、CartPoleより難しい問題になっています。 MountainCar は、強化学習界での Hello World 的な CartPole 問題ほど有名ではないけど、教科書などでも取り上げられているため、強化学習を始めたばかりの人もチャレンジするのではないでしょうか。

しかし！ OpenAI Gym で提供されている MountainCar-v0 を試すと、結構難しい問題だということに気づくはずです。
今提供されているバージョンは、設定が以前よりかなりシビアになっているんです。
昔のバージョンでは、ステップ数に限界がなく、車が目的地につくまでは done の判定がされなかったのですが、
現在のバージョンでは、エピソードの終了条件が、目的地到着または200ステップ経過、になっています。
これは、かなりキツイ。

初期のエージェントは馬鹿なので、ほぼランダムプレイしかできません。ランダムプレイでは、200ステップ以内に目的地に到着する確率は非常に小さいのにもかかわらず、報酬を得るのは目的に到着した時だけなので、学習の最初の手がかりを得ることが異常に難しい。
というわけで、このバージョンは全然初心者向きでないというより、難しい部類に入ってしまうのではないかと感じています。
（余談：なんでOpenAI はこんな変更したんだろう。強化学習の練習問題のはずだったのに。）

逆に言うと、このように正規の報酬が得られにくい状況は、内発的報酬を与えるこの論文の手法検討には適していると考えました。
（Atariのゲームでの検証は、GPUも積んでない自宅の貧弱PCでは満足な学習ができないってのも理由のひとつ。）

手法について

元論文はこちら

[1810.12894] Exploration by Random Network Distillation

この論文で提案されている手法は、いわゆる Curiosity Driven 方式です。エージェントが経験したことがない状況に対して高い内発的報酬を与えることで、未知の状態の探索行動を促進します。

この論文で提案されている手法の良い点は、その内発的報酬を与える仕組みが非常に簡単なことです。普通の発想だと、今まで経験したことのある状態を記憶したりカウントしたりして、経験したことがない状況を判定しようというアルゴリズムを作りたくなってしまいますが、この論文では、ある意味、逆の発想をしています。

彼らの提案した方法は、いわば、スクラッチ形式の地図のようなものだと、私はとらえました。
スクラッチって、あの、宝くじとかで使われている、あのスクラッチです。
状態空間の地図全体がスクラッチ前の銀紙で覆われていて、どこに何が埋まっているか分からないけれど、状態を経験するたびに、それに相当する部分だけが徐々に削れて浮かび上がってくる感じです。スクラッチが削れてしまったところは十分に経験したことがある状態で、まだ隠れている部分はまだ未経験の状態です。もし、十分に銀紙がはがれていない状態を経験したら、その時には、不透明度の度合いで報酬を与えることにします。（透明で見えてしまっているところは零点です。）

論文では、もちろん、上のような述べ方はしていません。論文では、Random Network Distillation (RND)と命名してきちんとした説明がされています。

エッセンスを伝えると、まず、2種類のネットワーク( $\hat{f}, f$ )を用意します。 $\hat{f} : s \rightarrow R^k$ は、target network、 $f : s \rightarrow R^k$ は、prediction network と呼びます。ここで $\hat{f}$ は最初にランダムに初期化した後は、手を付けずそのまま固定します。 target network によって、状態 $s$ はある埋め込み空間のベクトル $e_s \in R^k$ に移ります。

一方で、もう一つの prediction network はランダムに初期化された後、target network の出力を予想するように徐々にチューニングしていきます。つまり、ある状態 $s$ を経験するたびに、予測のずれ $L := \left | \hat{f}(s) - f (s) \right |^2$ を小さくするように、 $f$ を、少しずつ勾配降下法でチューニングいきます。

そして、この誤差 $L$ を、そのまま内発的報酬としてしまうのです。

似たような状態を経験するたびに、その状態に関して勾配降下法でネットワークの予測誤差が減っていきますので、内的報酬も減っていきます。一方で、まだ経験したことのない状態に関しては prediction network 出力のチューニングは不十分で予測誤差が大きいままですので、大きな内発的報酬が与えられるという仕組みです。

内発的報酬の計算方法に関する提案ですので、様々な既存の強化学習アルゴリズムに適用することが可能です。

テスト結果

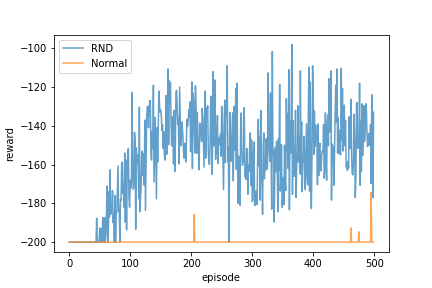
RNDを利用した内発的報酬を加えた場合と、加えない場合とで、（外発的）報酬の上がり方を示したのが下のグラフです。学習手法には Double Deep Q-Learning を使用しました。 RNDを用いたほうが、早くゴールにたどり着いて外発的報酬を得ることに成功していますので、問題を解くまでにかかる試行回数が少なくなっています。
というか、500試行程度では素のDouble DQNでは解けていません。
RNDの効果アリでした。 f:id:FakeOwl:20181126213957p:plain

チューニング

ただし、この結果になるまでには少々工夫も必要でした。論文でも書かれているように、内発的報酬のスケーリングを工夫しないと、予測誤差を素直に内発的報酬にするだけでは上手くいきませんでした。
RNDの更新の頻度や学習率なども上手く調整する必要がありそうです。また、内発的報酬を大きくしすぎると、おそらく Exploration/Exploitation バランスが崩れてしまうため、適度の内部報酬となるようにチューニングが必要であると思われます。
最終的には、今回の形式での内発的報酬は経験を積むにつれてゼロに近づくので、本来の外発的報酬だけが残るとは思いますが、それまでのスケジューリングを決めるのは大切なチューニング項目になりそうです。

MountainCar 程度でも試行錯誤が必要でしたので、Atari のゲームのように学習が重たいものを相手にするには、結構な計算リソースが必要になりそうな予感がします。

2018-10-20

「対角化の計算はできるんだけど、何をやっているのかイマイチ腑に落ちていない」という方は読んでみて欲しい。

線形代数

「対角化の計算はできるんだけど、何をやっているのかイマイチ腑に落ちていない」という方は読んでみて欲しい。

この投稿では、対角化の一連の計算がどのような意味を持つのかを説明する。

前回の基底変換に関する投稿： fakeowl.hatenablog.com を見ていない人は、まずはこちらを読んでいただけると理解が早いはずです。

対角化

$n$ 次元ベクトル空間 $V$ 上の線形変換 $\mathbb T$ を考える。 $T \in {\mathbb R}^{n \times n}$ は、基底 ${{\mathbf e}_1, {\mathbf e}_2, \cdots {\mathbf e}_n}$ による $\mathbb T$ の行列表現であるとする。このとき、 $T$ を対角化するとは、 $\hat{T} = P^{-1} T P$ が対角成分のみをもつように、 $P \in {\mathbb R}^{n \times n}$ を選び、具体的に $\hat{T}$ を作ることであった。

これは、一体何をしているのか。
一言で言うと、 ${{\mathbf e}_1,{\mathbf e}_2, \cdots, {\mathbf e}_n}$ とは別の基底を用いて、線形変換 ${\mathbb T}$ の表現行列 $\hat{T}$ を求めたのである。その際、上手に基底を選んで、 $\mathbb T$ の表現行列が対角行列になるようにしたのだ。

なぜ、こんなことをするのか？って、そりゃあ、同じ変換を扱うのであれば、その取り扱いが楽な方がいいに決まっている。対角行列は、すごく計算が楽だから扱いやすいし、見通しも良くて理解しやすい。だから、表現行列が対角行列になるような基底を探しだして、その基底での表現に取り替えてしまいたいのだ。対角化の手順は、そんな便利な基底を探しだす手順と、基底の取り換え手順の一連の操作によって与えられている。

対角化の手順は以下のとおりだ。

変換 ${\mathbb T}$ が簡単に見えるような、基底を見つける。
もとの基底から、新たな基底での表現に乗り換える。

では、次から、順にこの手順を説明してみよう。

変換が簡単に見える基底を見つける

まず、適当な基底 ${{\mathbf e}_1,{\mathbf e}_2, \cdots, {\mathbf e}_n}$ を入れて表現行列 $T$ を作る。
この表現行列 $T$ は、普通、対角行列なんかじゃなく、ぎっちりと非ゼロの成分がつまった行列のはずだ。だから、 $T$ による変換後のベクトルがどうなるかは、直感的には把握できそうにない。

では、直感的に把握できるような簡単な変換とは、どのようなものであろうか。
もっとも良い（簡単な）のは、「無変換」である。つまり、何の変化もないことだが、そんなことにはなろうはずもない（無変換なら、どんな基底を持ってきても、表現行列は最初から単位行列のはずだ。これ以上簡単な表現を探す必要もない）。

次に簡単な変換は、スカラー倍だと思う。単にベクトルにスカラーが掛かるだけ。（もっとも素朴なイメージとしては、ベクトルの方向は変わらないで、長さだけ伸び縮みするという変換。　実は、これは言い過ぎなので、最後の節で何をゴマかしたかは説明するが、当面はこのイメージで良いと思う。）
でも、そんな都合のいいように見える基底が存在するのだろうか？

実際に、そんな都合の良い基底があるのかどうか、探してみよう。
探したい基底ベクトルが満たすべき条件は、「変換しても向きが変わらず、伸び縮みだけしている」、ということなので、求める基底ベクトルの一つを ${\mathbf f}$ 、（まだ分からない）倍率を $m$ とすると、満たすべき条件は次のように書ける。 $$ T {\mathbf f} = m {\mathbf f} $$

しかし、ちょっと待て。上の式をちょっと変形してみると、 $$ (T - m I) {\mathbf f} = {\mathbf 0}. $$ （ $I$ は単位行列）

これはまずい。上の方程式を解くと、 ${\mathbf f} ={\mathbf 0}$ が出てきてしまって、終了。無念である。これでは基底にならない。

普通はここで引き下がるのだが、数学者というのは偉いものだ。ここで引き下がらなかった。次に彼らはどうしたのか。
「方程式が解けてしまうからダメだった。方程式が解ける限り、自明な解しか出て行こない。だったら、まともに解けない方程式であったらどうだろう」と考えた。
まともに解けないとは、「解が存在しない」とか「解が一意に定まらない」とかいうシチュエーションのことだ。
分かりやすい例としては、未知数が2こあるのに、関係式が１つしかない場合。この場合、解は無数に定まらず、無限にある。（例： $x, y$ に対して、方程式： $x + y = 1$ が与えられている場合、 $(x,y) = (0, 1), (2, -1), \cdots$ などと、無限に解がある。）
一意ではないかもしれないが、 ${\mathbf f} = {\mathbf 0}$ よりはマシである。他にもっとおもしろい解があるのかもしれないのだ。

というわけで、考えている方程式に、解が一意に定まらないように要求してみよう。行列 $T - mI$ に、逆行列が存在する場合、解は、 ${\mathbf f} = (T - m I)^{-1} {\mathbf 0} = {\mathbf 0}$ と求まってしまうので、行列 $T - mI$ が、逆行列を持たないように要求しよう。この条件は、 $$ \det (T - m I) = 0 $$ である。（この式は固有方程式と呼ばれている。）

行列 $T$ は与えられているものなので、 $m$ をうまく調整して固有方程式を満たすようにしたい。今、 $T$ は $n$ 次の正方行列なので、固有方程式は $m$ に関しては $n$ 次方程式となる。 $n$ 次方程式は、複素数の範囲で（重解を入れて）必ず $n$ 個の解を持つ。よって、必ず、解が一意に定まらないように出来るのだ。今、この固有方程式を解いて、解が $m_1, m_2, \cdots, m_n$ と得られたとしよう。すると、解 $m_i$ に対して、 $$ T {\mathbf f}_i = m_i {\mathbf f}_i $$ を満たすベクトル ${\mathbf f}_i$ を見つけることができる。ただし、一意に定まらないことはお忘れなく（ベクトルが一意に定まらないように $m_i$ を調整したのは、自分だ！）。一意に定まらないので、無限にある解のうちから好きな解を適当にチョイスしておけば良い。

さあ、これで望んだベクトル ${ {\mathbf f}_1, {\mathbf f}_2, \cdots, {\mathbf f}_n }$ が手に入った。これを基底にすれば、 ${\mathbb T}$ による変換は楽チンである。これを見るのは簡単だ。

固有ベクトルで作った基底を用いてベクトルを展開して ${\mathbf a} = \tilde{a}^1 {\mathbf f}_1 + \tilde{a}^2 {\mathbf f}_2 + \cdots + \tilde{a}^n {\mathbf f}_n$ と書けば、このベクトルに対する線形変換 ${\mathbb T}$ は $$ T {\mathbf a} = T (\tilde{a}^1 {\mathbf f}_1 + \cdots + \tilde{a}^n {\mathbf f}_n) \ = \tilde{a}^1 T({\mathbf f}_1) + \cdots \tilde{a}^n T({\mathbf f}_n) \ = \tilde{a}^1 m_1 {\mathbf f}_1 + \cdots \tilde{a}^n m_n {\mathbf f}_n $$ と計算できる。簡単だ！

つまり、 ${ {\mathbf f}_1, {\mathbf f}_2, \cdots, {\mathbf f}_n }$ を基底にすると、線形変換 ${\mathbb T}$ の表現行列 $\tilde T$ は、対角行列 $$ \tilde{T} = \begin{pmatrix} m_1 &&& \\ & m_2 && \\ && \ddots & \\ &&& m_n \\
\end{pmatrix} $$ となる。

基底の取り換え

前節で作った $\tilde{T}$ と、最初に適当に入れた基底での表現行列 $T$ との関係を見てみよう。

これを見るためには、同じ変換 ${\mathbb T}$ を基底： ${ {\mathbf f}_1, {\mathbf f}_2, \cdots, {\mathbf f}_n }$ での表現で行うことと、基底： ${ {\mathbf e}_1, {\mathbf e}_2, \cdots, {\mathbf e}_n }$ での表現で行うこととで見比べてみれば良い。

基底： ${ {\mathbf e}_1, {\mathbf e}_2, \cdots, {\mathbf e}_n }$ から基底： ${ {\mathbf f}_1, {\mathbf f}_2, \cdots, {\mathbf f}_n }$ への変換行列は $$ P = ({\mathbf f}_1, {\mathbf f}_2, \cdots, {\mathbf f}_n) $$ であり、ベクトルの成分は、 $$ \begin{pmatrix} \tilde{a}^1 \\ \vdots \\ \tilde{a}^n \\ \end{pmatrix} = P^{-1} \begin{pmatrix} a^1 \\ \vdots \\ a^n \\ \end{pmatrix} \leftrightarrow \begin{pmatrix} a^1 \\ \vdots \\ a^n \\ \end{pmatrix} = P \begin{pmatrix} \tilde{a}^1 \\ \vdots \\ \tilde{a}^n \\ \end{pmatrix} $$ の関係で結ばれる。

よって、基底： ${ {\mathbf f}_1, {\mathbf f}_2, \cdots, {\mathbf f}_n }$ の世界での変換 $\tilde{T}$ は、基底： ${ {\mathbf e}_1, {\mathbf e}_2, \cdots, {\mathbf e}_n }$ での世界での迂回ルートを通るとことにすると、

変換対象のベクトルを基底： ${\mathbf e}$ での表現に変換： $P$
基底： ${\mathbf e}$ の世界で変換： $T$
基底： ${\mathbf f}$ の世界に戻る： $P^{-1}$

の過程を通過するので、 $$ \tilde{T} = P^{-1} T P $$ となる。

いかがだろう。変換行列を固有ベクトルで作った行列（とその逆行列）で挟むと対角化されるということが、一連の迂回プロセスとして理解できるということが分かっただろうか。

逆ルートでも考えてみると、また少し理解が深まるかもしれないので、蛇足かもしれないが、そちらも書いておこう。
基底： ${\mathbf e}$ では変換が考えにくいので、

まず、ベクトルを基底： $f$ の世界で表現する。( $P^{-1}$ )
基底： ${\mathbf f}$ の世界で変換　（ $\tilde{T}$ )
基底： ${\mathbf e}$ の世界に戻す　（ $P$ )

このルートを通ると、 $$ T = P \tilde{T} P^{-1} $$ よって、 $$ \tilde{T} = P^{-1} T P $$

繰り返しになるが、対角化の計算は、

変換行列が簡単に見える（表現行列が対角行列になる）ようなベクトル（固有ベクトル）を探しだし、
そのベクトルで作った基底で変換行列を表現する

というプロセスなのである。

ごまかしたこと

今までの説明では、結構いろいろとぶっ飛ばした。この投稿では、数学的に細かいところはおいといてイメージを掴んでもらえれば良いのだけれど、それにしても乱暴な説明をした箇所があるので、そこについて補足しておこうと思う。

固有値と固有ベクトルは実数値ではない（かもしれない）

固有ベクトルを探す際に、「変換で向きが変わらず長さが変わるだけ」と言ってしまった。でも、このイメージは間違いである。固有値が実数であればイメージ通りだけど、固有値が実数とは限らない。固有方程式の解は、「複素数の範囲」で解が見つかるのだから、固有値が実数であるという保証はどこにもないのだ。

複素数というと、「私は実数の範囲の行列しか扱わないので必要ないっす」と思う人もいるかもしれないが、そうはいかない。実数の行列で表現される代表的な変換に回転変換があるが、これを考えてみると良い。「回転」変換をさせるのに、「向きが変わらず、伸び縮みするだけ」の変換を受けるようなベクトルがあるわけがない。実際に(正規直交基底での)回転変換行列： $R$ $$ R = \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \\ \end{pmatrix} $$ の固有方程式は、 $$ (\cos \theta - m)^2 + \sin ^2 \theta = 0 $$ なので、固有値は $$ m = \cos \theta \pm i \sin \theta = e^{\pm i \theta} $$ 固有ベクトルは $$ (1, -i)^T, (1,i)^T $$ であり、実数の範囲では解がない。

そもそも対角化できないかもしれない

固有ベクトルで基底を作るといったけれど、固有ベクトルが必ず $n$ 個あるとは限らない。
固有方程式が重解を持った時に、その重解の重複度と同じ本数の固有ベクトルが見つかれば良いが、見つからない時もあるのだ。その時は、対角行列で表現するような変換はできない・・・。あきらめよう！
（対角行列ほどではないけれど、次に扱いやすい形（ジョルダン標準形）に変換する方法もあるが、それは高度な話。）

この投稿で対角化の計算の意味がスッキリしたという人がいたら、うれしいです。
内積空間の話をすると、また別の角度からも見れてクリアになるので、その話も追々できたらと思っています。
それでは、今回はこのへんで。

2018-10-11

Reinforcement Learning for Improving Agent Design ：エンジニアが忘れてはいけないことを思い出させてくれた。

Reinforcement Learning

David Ha, Reinforcement Learning for Improving Agent Design のメモ

https://arxiv.org/abs/1810.03779

この論文では、総報酬を最大化するために、エージェント側の政策だけでなく、環境側も一緒に更新してしまおうという試みが紹介されている。

論文内の例題では、二足歩行ロボットをうまく制御するというタスクと同時に、タスク達成が用意になるようにロボットのデザインを調整している。

この試みは、強化学習という定式化の枠組みからは外れているけれど、現実世界への強化学習の応用を考えると、非常に興味深い。

というか、素敵だ。

自動デザインじゃないか、これ。

こういうアイデアは、アカデミアからでなく応用現場からでて欲しいとも思うので、メーカーに務める者としては、「やられたなぁ」という感じ。

（著者は Google Brain 所属なので、アカデミアではないといえばそうなのだが・・・）

普通、強化学習の問題設定は、

与えられた環境のもとで、
エピソード終了までの総報酬を最大化するような

行動を生成する政策を見つけよ、となっている。

一方で、製品開発の現場では、目的を達成するためならば達成手段を選ばない。
満たすべき制約を満足しているならば、どんな方法を使おうが構わない。
とにかく、目的を達する製品であれば良いのだ。

その考え方からすると、目的は報酬を最大化すればよいのであって、制約条件さえ満たしていれば環境側だって最適化の対象として良い。
ある製品がより良い価値を人間に提供するのであれば、価値を増やす責任を制御方法（政策）にだけ押し付けず、製品デザインにも手を加えるのは当然だ。　
「そもそも、設計がなってないのに、制御でなんとかしろって言われてもねぇ」と制御屋さんが愚痴をこぼすのはよくあることだけど、これはそのとおりで、本来は制御屋さんと設計屋さんとが一緒になって、目的達成のための最良のデザインと制御方法とを議論すべきなのである。

この論文は、その製品開発のワイルドさ（目的達成のためには、利用可能なあらゆる手段を用いて良い。当然、制御方法以外でも改善すべきことは改善する）を思い出させてくれたし、自動デザインにもつながるアイデアであって、久しぶりに新鮮な感動を味わわせていただいた。

感謝。

2018-10-08

EPISODIC CURIOSITY THROUGH REACHABILITY のメモ

Reinforcement Learning

N.Savinov (Google Brain), et.al, "EPISODIC CURIOSITY THROUGH REACHABILITY"

[1810.02274] Episodic Curiosity through Reachability

をナナメ読みしたメモ。

　概要

強化学習中に観測された状態が、過去に経験済みの状態と大きく離れているか（状態間を移り変わるまでに多くのステップが必要か）を判定する仕組み（Episodic Curiosity (EC) module）を提案している。 EC module によって観測した状態の目新しさが判定できるので、その目新しさに応じたボーナス報酬を本来の報酬に加えることで未知の状態への探索を促すというもの。

処理の概要

EC module の部品は４つ。

Embedding network
Comparator network
Episodic memory
Reward bonus estimation module

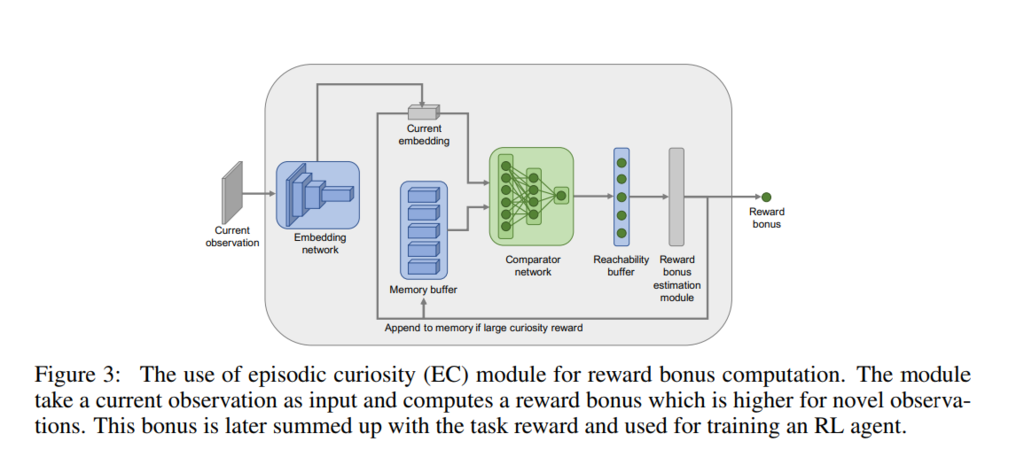f:id:FakeOwl:20181008231247p:plain (N.Savinov (Google Brain), et.al, "EPISODIC CURIOSITY THROUGH REACHABILITY", Fig.3)

Embedding network

状態量 $o$ を圧縮して内部表現 $e$ を出力するネットワーク: $e = E(o)$ 。論文の例題では ResNet-18 が使用されている。

Comparator network

Embeddingされた状態 $e_i, e_j$ 間の距離を互いの状態に移り変わるまでに必要なステップ数で定義し，そのステップ数があらかじめ決めておいた閾値 $k_{th}$ を超えたか否かで類似度(similarity score): $C(e_i, e_j) \in [0, 1$ ] を計算する。学習には cross entropy lossを使用する。

Episodic memory

Embedding された過去の観測量を保存するメモリーバッファー。メモリーには限りがあるので、足りなくなったらランダムに過去のものを捨てて入れ替える。

Reward bonus estimation module

エピソードバッファー中の全ての状態 $M=(e_1, e_2, \cdots, e_m)$ と現在の状態 $e$ との類似度 $c_i = C(e_i, e)$ をComparator network で計算し、 Reachability buffer に保管する。その後、aggregation 関数 $F(c_1, c_2, \cdots, c_m) \in [0, 1$ ]を用いて、現在の状態との類似度を計算する（理論的にはmax関数がよさそうであるが、90パーセンタイル値を用いるほうが成績が良かったらしい）。この類似度に応じて本来の報酬とは別のボーナス報酬: b を計算する。（バッファー中の全状態（論文ではメモリーサイズ $m$ は200に設定してある）に対して現在の状態との類似度計算するので処理は重たいのでは？学習時だけなので大きなでは問題ないとも思う。）

2018-09-26

基底を取り換えると行列表示はどう変わる？

線形代数

基底を取り替えたらどうなるのか

線形代数に関する前の投稿

fakeowl.hatenablog.com

の続き。
それでは具体的に、基底の取り方を変えた時にどのように変換行列が変わるのかを見ていこうと思う。

入力側の基底の変換

まずは、入力側の基底を取り替えてみよう。前の投稿で例に上げた、基底１を「つまみＡを時計回りに１度回すこと」から、「つまみＡを時計回りに２度回すこと」と変えることを、詳しく見てみよう。この場合、新しい基底： ${\mathbf e}' _ 1$ は、元の基底を使って $$ {\mathbf e}'_1 = 2 {\mathbf e}_1 $$ と書ける。基底 ${\mathbf e}_1$ だけ取り替えるというのは一般的でないので、基底 ${\mathbf e}_2$ も基底 ${\mathbf e}_3$ も恒等変換（何もしないという変換）していると考えて ${\mathbf e}'_2 = {\mathbf e}_2, {\mathbf e}'_3 = {\mathbf e}_3$ としておこう。行列表現を考えるということは、すべてのベクトルを考えている基底での成分で表現するということである。元の基底で $(a^1, a^2, a^3)^T$ と成分表示されていたベクトルの成分は、基底を取り換えたときどのように変化するだろうか。ここでもう一度思い出して欲しいのは、基底の決め方と、表したい状態（ここでは、３つのつまみがどの角度になっているのかということ）とは関係ないということ。もとの基底で $(a^1, a^2, a^3)^T$ という成分で表されているのは、つまみＡ、つまみＢ、つまみＣの角度が、それぞれ、 $a^1$ 度、 $a^2$ 度、 $a^3$ 度であることに対応する。今、基底１を取り替えて、新しい基底が ${\mathbf e}'_1=2 {\mathbf e}_1$ であるということは、同じ状態を新旧の基底で表すと、

$$ a^1 {\mathbf e}_1 + a^2 {\mathbf e}_2 + a^3 {\mathbf e}_3 = \frac{a^1}{2} {\mathbf e}'_1 + a^2 {\mathbf e}'_2 + a^3 {\mathbf e}'_3 $$

となる。新しい基底１が、もとの基底１の２倍の角度を表すことになったことを打ち消すように、対応する成分は 1/2 に変化しなければならない。そうしないと、同じベクトルを表すことにならないからだ。基底の変換に伴う、行列表現の変換の本質はこの例に尽きる。

これを一般化して表現していこう。新しい基底： ${ {\mathbf e}' _ 1, {\mathbf e}'_ 2, {\mathbf e}'_ 3}$ を、元の基底を使って $$ {\mathbf e}'_ 1 = p^1_1 {\mathbf e}_1 + p^2_1 {\mathbf e}_2 + p^3_1 {\mathbf e}_3 \\ {\mathbf e}'_ 2 = p^1_2 {\mathbf e}_1 + p^2_2 {\mathbf e}_2 + p^3_2 {\mathbf e}_3 \\ {\mathbf e}'_ 3 = p^1_3 {\mathbf e}_1 + p^2_3 {\mathbf e}_2 + p^3_3 {\mathbf e}_3 $$ と作ったとしよう（新旧の基底を結ぶ関係式）。基底を取り替えたとしても、表したい状態ベクトルが変わるわけではない。そして、新しい基底の線型結合でも同じベクトルを表せるはずだ。つまり、 $$ a^1 {\mathbf e}_1 + a^2 {\mathbf e}_2 + a^3 {\mathbf e}_3 = a'^1 {\mathbf e}'_ 1 + a'^2 {\mathbf e}'_ 2 + a'^3 {\mathbf e}'_ 3
$$ を満たす新しい基底での成分 $(a'^1, a'^2, a'^3)^T$ があるはずだ。基底の取り換えの式（新旧の基底を結ぶ関係式）を使うと、

\begin{align} & a'^1 {\mathbf e}'_ 1 + a'^2 {\mathbf e}'_ 2 + a'^3 {\mathbf e}'_ 3 \\ &= a'^1 (p^1_1 {\mathbf e}_1 + p^2_1 {\mathbf e}_2 + p^3_1 {\mathbf e}_3) \\ &\quad + a'^2 (p^1_2 {\mathbf e}_1 + p^2_2 {\mathbf e}_2 + p^3_2 {\mathbf e}_3) \\ &\quad + a'^3 (p^1_3 {\mathbf e}_1 + p^2_3 {\mathbf e}_2 + p^3_3 {\mathbf e}_3) \\ &= (a'^1 p^1_1 + a'^2 p^1_2 + a'^3 p^1_3) {\mathbf e}_1 \\ &\quad + (a'^1 p^2_1 + a'^2 p^2_2 + a'^3 p^2_2) {\mathbf e}_2 \\ &\quad + (a'^3 p^3_1 + a'^2 p^3_2 + a'^3 p^3_3) {\mathbf e}_3 \end{align}

なので、成分同士を見比べて、新旧のベクトルの成分の関係が次のようになっていることがわかる。 $$ a^1 = a'^1 p^1_1 + a'^2 p^1_2 + a'^3 p^1_3 \\ a^2 = a'^1 p^2_1 + a'^2 p^2_2 + a'^3 p^2_2 \\ a^3 = a'^3 p^3_1 + a'^2 p^3_2 + a'^3 p^3_3 $$

これらの変換関係は、行列を用いるとコンパクトに書ける。 $$ P = \left( \begin{matrix} p^1_1 & p^1_2 & p^1_3 \\ p^2_1 & p^2_2 & p^2_3 \\ p^3_1 & p^3_2 & p^3_3 \end{matrix} \right) $$ とすると、新旧の基底の変換関係は、 $$ ({\mathbf e}'_1, {\mathbf e}'_2, {\mathbf e}'_3) = ({\mathbf e}_1, {\mathbf e}_2, {\mathbf e}_3) P $$ と書けるし、成分の変換関係は、 $$ \left( \begin{matrix} a^1 \\ a^2 \\ a^3 \end{matrix} \right) = P \left( \begin{matrix} a'^1 \\ a'^2 \\ a'^3 \end{matrix} \right)
$$ と書けるので、新しい成分を古い成分で表すならば、 $$ \left( \begin{matrix} a'^1 \\ a'^2 \\ a'^3 \end{matrix} \right) = P^{-1} \left( \begin{matrix} a^1 \\ a^2 \\ a^3 \end{matrix} \right)
$$ である。古い基底から新しい基底への変換行列を $P$ としたとき、古い成分から新しい成分への変換行列が $P$ の逆行列 $P^{-1}$ となる意味は、もうおわかりだろう。同じベクトルを表そうとしているのに、基底だけを取り替えて成分をほったらかしにしたら、表しているベクトルが変わってしまうので、基底が変わった分の変化を打ち消すように成分が変化しなければならない。それで、基底と成分の変換関係が互いに逆になっているのである。

出力側の基底の変換

もちろん、出力側の基底も自由に取り替えることができる。今回の例では、出力側の次元が２次元であること以外は、入力側の議論と全く同じであるので説明は省略するが、基底の変換行列を $$ Q = \left( \begin{matrix} q^1_1 & q^1_2 \\ q^2_1 & q^2_2 \end{matrix} \right) $$ とすると、新旧の基底の関係は $$ ({\mathbf E}'_ 1, {\mathbf E}'_ 2)=({\mathbf E}_1, {\mathbf E}_2)Q $$ であり、成分の関係は $$ \left( \begin{matrix} b'^1 \\ b'^2 \end{matrix} \right) = Q^{-1} \left( \begin{matrix} b^1 \\ b^2 \end{matrix} \right) $$ である。

入出力の基底を同時に取り換え

入力側も出力側も両方取り替えたって、もちろん構わない。このとき、新しい基底での入出力の変換行列はどのように変わるのかを見ていこう。

古い基底での入出力の関係が次のように書けているものとする。 $$ \left( \begin{matrix} b^1 \\ b^2 \end{matrix} \right) = T \left( \begin{matrix} a^1 \\ a^2 \\ a^3 \end{matrix} \right) $$ ここで、 $$ T = \left( \begin{matrix} t^1_1 & t^1_2 & t^1_3 \\ t^2_1 & t^2_2 & t^2_3 \end{matrix} \right) $$ である。

もとの基底での入出力の関係がわかっているので、これを新しい基底での入出力の関係に焼き直していこう。入力側、出力側の成分の変換はわかっているので、それを代入すると $$ Q \left( \begin{matrix} b'^1 \\ b'^2 \end{matrix} \right) = T P \left( \begin{matrix} a'^1 \\ a'^2 \\ a'^3 \end{matrix} \right) $$ なので、すこし式を変形して $$ \left( \begin{matrix} b'^1 \\ b'^2 \end{matrix} \right) =Q^{-1}TP \left( \begin{matrix} a'^1 \\ a'^2 \\ a'^3 \end{matrix} \right) $$ が得られる。つまり、新しい基底での入出力の関係を表す変換行列 $T'$ は、 $$ T' = Q^{-1} T P $$ である。